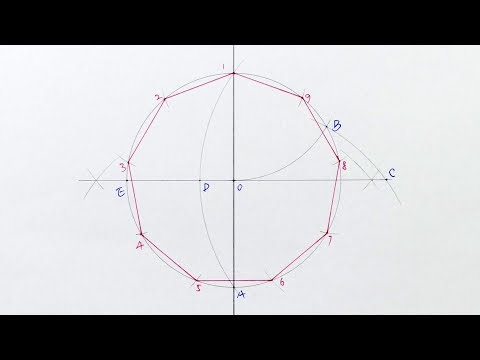
Définition et propriétés de l’enneagon
Un enneagon est une figure plane à neuf côtés égaux, également appelée nonogone, qui présente des propriétés géométriques spécifiques.
Les angles internes d’un enneagon régulier mesurent 140 degrés, tandis que les sommets forment des angles de 40 degrés.
Introduction
L’enneagon, également connu sous le nom de nonogone, est un polygone à neuf côtés qui appartient à la famille des figures planes.
Cette figure géométrique possède des propriétés particulières qui en font un objet d’étude intéressant en mathématiques élémentaires.
L’enneagon peut être régulier ou irrégulier, selon que ses côtés et ses angles soient égaux ou non.
La construction géométrique d’un enneagon peut se faire de différentes manières, en utilisant des outils tels que la règle et le compas, ou des méthodes plus avancées impliquant des calculs trigonométriques.
Malgré sa relative complexité, l’enneagon est une figure géométrique fascinante qui apparaît dans de nombreux contextes, de la nature à l’architecture et au design.
Ce chapitre aura pour but d’exposer les propriétés et les caractéristiques de l’enneagon, ainsi que les méthodes de construction et les exemples d’applications de cette figure géométrique.
Propriétés géométriques
Les propriétés géométriques de l’enneagon sont liées à sa structure et à ses dimensions.
Un enneagon régulier est caractérisé par neuf côtés égaux et neuf angles internes égaux, dont la mesure est de 140 degrés.
La somme des angles internes d’un enneagon est égale à 1260 degrés, ce qui est une propriété commune à tous les polygones.
Les diagonales d’un enneagon régulier sont également égales et leur nombre est de 27.
Les propriétés géométriques de l’enneagon permettent de calculer facilement sa surface et son périmètre, en fonction de la longueur de ses côtés.
Ces propriétés géométriques font de l’enneagon un objet d’étude intéressant en mathématiques élémentaires et permettent de résoudre des problèmes géométriques variés.
Elles sont également utiles pour les applications pratiques, comme la conception de formes et de structures architecturales.
Construction géométrique de l’enneagon
La construction géométrique de l’enneagon implique l’utilisation de règles et de compas pour tracer les neuf côtés égaux et les angles internes de 140 degrés.
Méthodes de construction
Il existe plusieurs méthodes pour construire un enneagon, notamment ⁚
- La méthode du cercle, qui consiste à inscrire le polygone dans un cercle et à diviser la circonférence en neuf parties égales.
- La méthode de la diagonale, qui implique de tracer les diagonales d’un carré et de les prolonger pour obtenir les côtés de l’enneagon.
- La méthode de la division, qui consiste à diviser un angle droit en neuf parties égales et à construire les côtés de l’enneagon à partir de ces angles.
Ces méthodes nécessitent une bonne maîtrise des concepts de base de la géométrie, tels que les angles, les côtés et les figures planes.
Il est important de noter que la construction d’un enneagon régulier nécessite une grande précision et une bonne compréhension des propriétés géométriques du polygone.
En résumé, la construction géométrique de l’enneagon requiert une solide formation en mathématiques élémentaires et une pratique assidue des techniques de construction géométrique.
Exemples de construction
Voici quelques exemples de construction d’enneagons réguliers et irréguliers ⁚
Exemple 1 ⁚ Construction d’un enneagon régulier à l’aide de la méthode du cercle ⁚
- Dessiner un cercle de centre O et de rayon r.
- Déterminer les points de division de la circonférence en neuf parties égales.
- Relier ces points pour former les côtés de l’enneagon.
Exemple 2 ⁚ Construction d’un enneagon irrégulier à l’aide de la méthode de la diagonale ⁚
- Dessiner un carré ABCD.
- Prolonger les diagonales pour obtenir les côtés de l’enneagon.
Ces exemples illustrent les différentes approches possibles pour construire un enneagon, qu’il soit régulier ou irrégulier.
Ils montrent également l’importance de la précision et de la rigueur dans la construction géométrique.
Exemples et applications de l’enneagon
L’enneagon apparaît dans certaines formes naturelles, comme les fleurs de lotus ou les coquilles de certains mollusques.
Exemples dans la nature
L’enneagon est présent dans certaines formes naturelles, révélant ainsi la présence de principes géométriques sous-jacents dans la structure de ces objets.
C’est le cas des fleurs de lotus, dont les pétales sont disposées selon une forme polygonale à neuf côtés.
Certaines coquilles de mollusques, comme la coquille de nautilus, présentent également une structure enneagonal.
Ces exemples montrent que la géométrie est omniprésente dans la nature et qu’elle guide la formation de certaines structures biologiques.
Ces observations ont inspiré les architectes et les designers, qui ont utilisé l’enneagon comme motif dans leurs créations.
L’étude de ces exemples naturels permet de mieux comprendre les principes mathématiques qui régissent la formation de ces structures.
Ces découvertes ont également des implications pour la compréhension de la symétrie et de la forme dans la nature.
Applications en architecture et en design
L’enneagon est utilisé dans divers domaines de l’architecture et du design pour créer des formes esthétiques et fonctionnelles.
Les architectes l’utilisent pour concevoir des bâtiments aux formes originales, tels que des musées, des bibliothèques ou des centres commerciaux.
En design, l’enneagon est employé pour créer des motifs décoratifs, des logos et des icônes.
Cette forme géométrique est également utilisée dans la conception de meubles et d’objets de décoration, tels que des tapis, des vases ou des luminaires;
L’enneagon est apprécié pour sa symétrie et sa régularité, qui confèrent une sensation d’équilibre et d’harmonie aux créations.
Les designers et les architectes exploitent ces propriétés pour créer des espaces et des objets qui inspirent la beauté et la fonctionnalité.
L’enneagon est donc un outil puissant pour les créateurs qui cherchent à exprimer leur imagination et leur créativité.
L’enneagon, cette figure plane à neuf côtés égaux, offre une richesse de propriétés géométriques et de applications pratiques.
Grâce à ses angles internes et ses sommets bien définis, l’enneagon régulier peut être construit avec précision et utilisation dans divers domaines.
Que ce soit en mathématiques élémentaires, en architecture ou en design, l’enneagon est un outil puissant pour créer des formes esthétiques et fonctionnelles.
Les exemples présentés dans ce chapitre montrent l’étendue des possibilités offertes par cette figure géométrique.
En résumé, l’enneagon est une figure plane fascinante qui combine beauté et fonctionnalité, rendant ses applications quasi infinies.
Ce chapitre a permis de mettre en avant les propriétés et les applications de l’enneagon, mais il est évident que cette figure géométrique recèle encore beaucoup de secrets et de potentialités à explorer.
Il est donc essentiel de continuer à étudier et à explorer les propriétés et les applications de l’enneagon pour en tirer le maximum de profit.